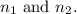Final Answer:
a)
 follows a normal distribution with mean 75 - 70 = 5 and standard deviation
follows a normal distribution with mean 75 - 70 = 5 and standard deviation
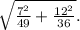
b) This probability is approximately 0.136, or 13.6%.
c) The values are
 = 60 and
= 60 and
 = 90. The sum is 150.
= 90. The sum is 150.
Step-by-step explanation:
(a) The probability distribution of
 is normally distributed with a mean equal to the difference of the population means
is normally distributed with a mean equal to the difference of the population means
 and a standard deviation equal to the square root of the sum of the variances divided by their respective sample sizes
and a standard deviation equal to the square root of the sum of the variances divided by their respective sample sizes
 follows a normal distribution with mean
follows a normal distribution with mean
 and standard deviation
and standard deviation
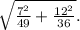
(b) To find the probability that
 , we standardize the values and then find the area under the standard normal curve between the z-scores corresponding to
, we standardize the values and then find the area under the standard normal curve between the z-scores corresponding to
 . Using the standard normal distribution table, we can calculate this probability.
. Using the standard normal distribution table, we can calculate this probability.
(c) If
 , we can determine the sample sizes
, we can determine the sample sizes
 by solving for them. By rearranging the formula for the standard deviation of
by solving for them. By rearranging the formula for the standard deviation of
 we can substitute in the given values and solve for
we can substitute in the given values and solve for