Answer:

Step-by-step explanation:
Because the function intersects its midline at
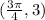 , then the midline is
, then the midline is
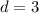 .
.
Additionally, the amplitude is just the positive distance between the maximum/minimum and the midline, so the amplitude is
 .
.
Also, given that period is
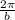 and the fact that the period is
and the fact that the period is
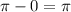 from our given maximum, we have the equation
from our given maximum, we have the equation
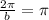 where
where
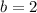 .
.
Lastly, to find
 , we know that the phase shift,
, we know that the phase shift,
 , is
, is
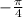 (or
(or
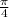 to the left) since
to the left) since
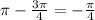 . Therefore, we have the equation
. Therefore, we have the equation
 where
where
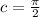 .
.
Putting it all together, our final equation is
