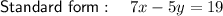Question

NO LINKS!! Please help me with this problem. Find a formula that expresses the fact that an arbitrary point P(x, y) is on the perpendicular bisector l of segment AB.​

Answer 1

`\textsf{Slope-intercept form}: \quad y=(7)/(5)x-(19)/(5)`

`\textsf{Standard form}: \quad 7x-5y=19`

Explanation:

A perpendicular bisector is a line that intersects another line segment at 90°, dividing it into two equal parts.

To find the perpendicular bisector of segment AB, find the slope of AB and the midpoint of AB.

Define the points:

• Let (x₁, y₁) = A(-5, 4)
• Let (x₂, y₂) = B(9, -6)

Slope of AB

`\textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(-6-4)/(9-(-5))=(-10)/(14)=-(5)/(7)`

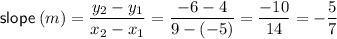
Midpoint of AB

`\textsf{Midpoint}=\left((x_2+x_1)/(2),(y_2+y_1)/(2)\right)=\left((9+(-5))/(2),(-6+4)/(2)\right)=(2,-1)`

If two lines are perpendicular to each other, their slopes are negative reciprocals.

Therefore, the slope of the line that is perpendicular to line segment AB is ⁷/₅.

Substitute the found perpendicular slope and the midpoint of AB into the point-slope formula to create an equation for the line that is the perpendicular bisector of line segment AB:

`\implies y-y_1=m(x-x_1)`

`\implies y-(-1)=(7)/(5)(x-2)`

`\implies y+1=(7)/(5)x-(14)/(5)`

`\implies y=(7)/(5)x-(14)/(5)-1`

`\implies y=(7)/(5)x-(19)/(5)`

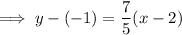
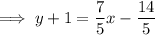
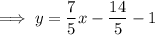
Therefore, the formula that expresses the fact that an arbitrary point P(x, y) is on the perpendicular bisector of segment AB is:

`\textsf{Slope-intercept form}: \quad y=(7)/(5)x-(19)/(5)`

`\textsf{Standard form}: \quad 7x-5y=19`

Answer 2

Given points

• A(-5, 4), B(9, - 6)

Find the midpoint of AB

• M = ((- 5 + 9)/2, (4 - 6)/2) = (2, -1)

Find the slope of AB

• m = (-6 - 4)/(9 + 5) = - 10 / 14 = - 5/7

The point P is on the perpendicular line to AB that passes through its midpoint.

We know perpendicular lines have opposite-reciprocal slopes.

So the line we are looking for has a slope of 7/5.

Use the point-slope equation to find the line:

• y - y₁ = m(x - x₁)
• y - (-1) = 7/5(x - 2)
• y + 1 = 7/5(x - 2) Point- slope form
• y = 7/5x - 19/5 Slope- intercept form
• 5y = 7x - 19
• 7x - 5y = 19 Standard form

Choose any form above of the same line.