Question

The y-coordinate of at’ is the same as R,

Answer 1

Since the x-coordinate of R is 7, the y-coordinate of R is equal to -4.

In Mathematics and Geometry, the point-slope form of a straight line can be calculated by using the following mathematical equation (formula):

`y - y_1 = m(x - x_1)`

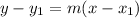
Where:

• x and y represent the data points.
• m represent the slope.

First of all, we would determine the slope of line PQ by using these points (5,-12) and (15,-6);

`Slope(m)=(y_2-y_1)/(x_2-x_1)`

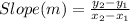
Slope (m) = (-6 + 12)/(15 - 5)

Slope (m) = 6/10

Slope (m) = 3/5

At data point (5, -12) and a slope of 3/5, an equation for line PQ can be calculated by using the point-slope form as follows:

y + 12 = 3/5(x - 5)

y = 3/5(x) - 15

For the midpoint of PQ, we have:

Midpoint PQ =
`((15+5)/(2) ,(-6-12)/(2) )`

Midpoint PQ = (10, -9)

Since the lines are perpeniduclar, the slope (m) of line l is given by;

m × 3/5 = -1

m = -5/3

At midpoint (10, -9) and a slope of -5/3, an equation for line l can be calculated by using the point-slope form as follows:

y + 9 = -5/3(x - 10)

y = -5/3(x) + 50/3 - 9

y = -5/3(x) + 23/3

When x is 7, the y-coordinate of R is given by;

y = -5/3(7) + 23/3

y = -35/3 + 23/3

y = -12/3

y = -4

Complete Question:

The points P and Q have coordinates (5,-12) and (15,-6) respectively. The point R lies on the line l, the perpendicular bisector of the line PQ. The x-coordinate of R is 7.

Find the y-coordinate of R.