Question

Given that f(x=Pass,y=5tuts)=0.51 What is the product of f(x=pass) and f(y=5tuts)?

Answer 1

The product of
`\( f(x=\text{Pass}) \) and \( f(y=5\text{Tuts}) \) is 0.51.`

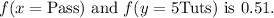
Step-by-step explanation:

The given function is
`\( f(x=\text{Pass}, y=5\text{Tuts}) = 0.51 \).` To find the product of
`\( f(x=\text{Pass}) \) and \( f(y=5\text{Tuts}) \)`, we substitute the respective values into the function. Since
`\( f(x=\text{Pass}, y=5\text{Tuts}) = 0.51 \)`, it implies that
`( f(x=\text{Pass}) * f(y=5\text{Tuts}) = 0.51 \).` This is because when one of the variables is fixed at its given value, the function becomes a constant, and multiplying it by the other constant value results in the same constant.

Understanding the product of these function values is essential in mathematical modeling and analysis. In this context, it could represent the joint probability or likelihood of both events
`\( x=\text{Pass} \) and \( y=5\text{Tuts} \)` occurring simultaneously. The product is a measure of the combined impact or occurrence probability of both events, and in this case, it is given by the constant value of 0.51.

In summary, the product of
`\( f(x=\text{Pass}) \) and \( f(y=5\text{Tuts}) \)` is 0.51, indicating the joint likelihood or impact of the events
`( x=\text{Pass} \) and \( y=5\text{Tuts} \)` in the given mathematical context.