Final Answer:
The x-intercept for the function
 is ( x = 0 ).
is ( x = 0 ).
Step-by-step explanation:
To find the x-intercept of a function, we set ( f(x) ) equal to zero and solve for ( x ). In this case, we have the equation
 . Factoring out the common factor of
. Factoring out the common factor of
 Setting each factor equal to zero gives us two possible solutions: ( x = 0 ) and
Setting each factor equal to zero gives us two possible solutions: ( x = 0 ) and
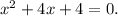
However, when we solve for ( x ) in the quadratic equation
 , we find that it can be factored into
, we find that it can be factored into
 . This yields a repeated root of ( x = -2 ). Therefore, the only distinct x-intercept is ( x = 0 ).
. This yields a repeated root of ( x = -2 ). Therefore, the only distinct x-intercept is ( x = 0 ).
In mathematical terms, the function
 has a triple root at ( x = 0 ) and a double root at ( x = -2 ). The repeated roots indicate that the graph touches the x-axis at these points without crossing it. Therefore, the final x-intercept for this function is ( x = 0 ).
has a triple root at ( x = 0 ) and a double root at ( x = -2 ). The repeated roots indicate that the graph touches the x-axis at these points without crossing it. Therefore, the final x-intercept for this function is ( x = 0 ).