Question

F(x)=-9x^(3)+3x^(2)+27x-9 Write your answer as a list of sim

Answer 1

• The critical points of the function
  `\( F(x) = -9x^3 + 3x^2 + 27x - 9 \) are \( x = -1 \) and \( x = 3 \)`.

• Using the first derivative test, we determine that
  `\( F(x) \)` has a local minimum at
  `\( x = -1 \)` and a local maximum at
  `\( x = 3 \).`

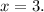
Step-by-step explanation:

The given function
`\( F(x) = -9x^3 + 3x^2 + 27x - 9 \)` can be analyzed to find its critical points, which are the values of
`x` where the derivative is equal to zero or undefined. To find these points, we take the derivative of
`\( F(x) \)` with respect to
`\( x \)`. Setting the derivative equal to zero and solving for
`\( x \)` gives us the critical points. In this case, the critical points are
`\( x = -1 \) and \( x = 3 \)`.

Next, we use the first derivative test to determine the nature of these critical points. By analyzing the sign of the derivative in the intervals defined by the critical points, we can identify whether the function has local maxima, minima, or points of inflection. In our case, for
`\( x = -1 \)`, the function
`\( F(x) \)` has a local minimum, and for
`\( x = 3 \)`, it has a local maximum.

Therefore, the final answer consists of identifying the critical points and using the first derivative test to characterize the nature of these points. This process provides valuable insights into the behavior of the function and is crucial for understanding its local extrema.