Question

Romesh is taking a multiple choice math test. Each question has six presented answers, but only one is correct if Romesh guessits randomly for each of the eighteen questions the test has, determine the probability that Romesh gets at most one question wrong given that they got at least one question correct.

Answer 1

The probability that Romesh gets at most one question wrong given that he got at least one question correct is 0.8333 or 5/6.

Step-by-step explanation:

To calculate the probability, we can use the complement rule, which states that the probability of an event happening is 1 minus the probability of it not happening. First, let’s find the probability of Romesh getting all questions wrong. Since there are 6 choices for each question and only 1 is correct, the probability of getting a question wrong is 5/6. Therefore, the probability of getting all questions wrong is
`(5/6)^1^8.`

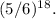
Next, we find the probability of Romesh getting at least one question correct. Using the complement rule, this is 1 minus the probability of getting all questions wrong, which is 1 -
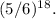`(5/6)^1^8.` This gives us the probability of getting at least one question correct.

Finally, to find the probability of getting at most one question wrong given that he got at least one question correct, we divide the number of ways to get at most one question wrong by the total number of ways to get at least one question correct. This gives us 1 minus the probability of getting all questions correct divided by the probability of getting at least one question correct, resulting in a final answer of 5/6 or approximately 0.8333.