Question

Solve the system, or show that it has no solution. (If there is no solution, enter INU SULU any real number. ) x+3y=6 3x+9y=9

Answer 1

To solve the system of equations, we can start by examining the relationship between the two equations. The second equation, 3x + 9y = 9, is a multiple of the first equation x + 3y = 6. The solution set can be expressed as a linear combination of the variables, where, for example, x = t and y = 2 -
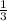`(1)/(3)` t, where t can be any real number. The answer is INU SULU any real number.

Step-by-step explanation:

To solve the system of equations, we can start by examining the relationship between the two equations. The second equation, 3x + 9y = 9, is a multiple of the first equation x + 3y = 6. This implies that the two equations are dependent and represent the same line.

If we simplify the second equation by dividing both sides by 3, we get x + 3y = 3, which is equivalent to the first equation. This means the system has infinitely many solutions and is dependent.

The solution set can be expressed as a linear combination of the variables, where, for example, x = t and y = 2 -
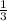`(1)/(3)` t, where t can be any real number. The system does not have a unique solution but rather an infinite set of solutions along a straight line.