Question

In the expression (ax⁵+bx+c)/(x−d)(x+e)​, it's considered an improper fraction. To make it proper, what is the degree of the polynomial that needs to be added to the expression?

Answer 1

To make the expression
`\((ax^5+bx+c)/((x-d)(x+e))\)` a proper fraction, you need to add a polynomial of degree 2 in the numerator.

Step-by-step explanation:

An improper fraction in the context of polynomial expressions typically refers to a situation where the degree of the numerator is equal to or greater than the degree of the denominator. In this case, the given expression has a numerator of degree 5 (due to the
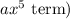`\(ax^5\) term)` and a denominator of degree 2 (due to the
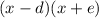`\((x-d)(x+e)\)` factors).

To make the fraction proper, the degree of the numerator needs to be less than the degree of the denominator. Adding a polynomial term of degree 2 to the numerator would reduce its degree to 4, making it proper in relation to the degree-2 denominator. The expression would then take the form
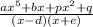`\((ax^5+bx+px^2+q)/((x-d)(x+e))\)`, where \(p\) and \(q\) represent coefficients of the added quadratic term.

Understanding the concept of proper and improper fractions in the context of polynomials involves recognizing the balance between the degrees of the numerator and denominator. Adjusting the degrees appropriately ensures a proper rational expression.