Question

Given: y varies jointly as a and b and inversely as the cube of c. Find y when a=8,b=8 and c=4 if y=21 when a=4,b=6, and c=2

Answer 1

`\(y = \frac{{ab}}{{c^3}}\)`

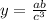
Given a=8, b=8, and c=4, substituting these values into the formula, we get
`\(y = \frac{{8 \cdot 8}}{{4^3}} = 4\)`.

Step-by-step explanation:

In this problem, we are dealing with a joint and inverse variation relationship. The formula for joint and inverse variation is
`\(y = k \cdot \frac{{ab}}{{c^3}}\)`, where k is the constant of proportionality. To find k, we can use the initial condition provided: y=21 when a=4, b=6, and c=2.

Substitute these values into the formula:

`\[21 = k \cdot \frac{{4 \cdot 6}}{{2^3}}\]`

Now, solve for \(k\):

`\[k = \frac{{21 \cdot 2^3}}{{4 \cdot 6}} = \frac{{168}}{{24}} = 7\]`

Now that we have the value of k, we can use it to find y when a=8, b=8, and c=4:

`\[y = 7 \cdot \frac{{8 \cdot 8}}{{4^3}} = 7 \cdot \frac{{64}}{{64}} = 7 \cdot 1 = 7\]`

Therefore, the final answer is y = 7, which represents the value of y when a=8, b=8, and c=4.