Question

If y = cos x, how many periods will there be between -5pi and 9pi ?

Answer 1

7 periods.

Explanation:

The cosine function is periodic, meaning it repeats forever.

Standard form of a cosine function:

`f(x) = A \cos(B(x + C)) + D`

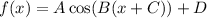
where:

• A = amplitude (height from the mid-line to the peak).
• 2π/B = period (horizontal distance between consecutive peaks).
• C = phase shift (horizontal shift - positive is to the left).
• D = vertical shift.

Therefore, for y = cos x:

• Amplitude = 1
• Period = 2π
• Phase shift = 0
• Vertical shift = 0

The maximum of the function is when x = 0 + 2πn.

The minimum of the function is when x = π + 2πn.

To find the number of periods, first find the difference between the two given values:

⇒ 9π - (-5π) = 9π + 5π = 14π

As the period of the function is 2π, then the number of periods is:

⇒ 14π ÷ 2π = 7 periods.