Question

9. The times of first sprinkler activation (in seconds) for a series of tests of fire-prevention sprinkler systems that use aqueous film-forming foam is as follows. The system has been designed so that the true average activation time is supposed to be at most 25 seconds. Does the data indicate the design specifications have not been met

Answer 1

This question is incomplete, the complete question is;

The times of first sprinkler activation (in seconds) for a series of tests of fire-prevention sprinkler systems that use aqueous film-forming foam is as follows; 27 41 22 27 23 35 30 33 24 27 28 22 24

( see " use of AFFF in sprinkler systems," Fire technology, 1975: 5)

The system has been designed so that the true average activation time is supposed to be at most 25 seconds.

Does the data indicate the design specifications have not been met?

Test the relevant hypothesis at significance level 0.05 using the P-value approach

Answer:

since p-value (0.042299) is lesser than the level of significance ( 0.05)

We Reject Null Hypothesis

Hence, There is no sufficient evidence that the true average activation time is at most 25 seconds

Step-by-step explanation:

Given the data in the question;

lets consider Null and Alternative hypothesis;

Null hypothesis H₀ : There is sufficient evidence that the true average activation time is at most 25 seconds

Alternative hypothesis H₁ : There is no sufficient evidence that the true average activation time is at most 25 seconds

i.e

Null hypothesis H₀ : μ ≤ 25

Alternative hypothesis H₁ : μ > 25

level of significance σ = 0.05

first we determine the sample mean;

`x^(bar)` =
`(1)/(n)`∑
`x_(i)`

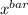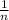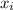
where n is sample size and ∑
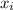`x_(i)` is summation of all the sample;

=
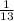`(1)/(13)`( 27 + 41 + 22 + 27 + 23 + 35 + 30 + 33 + 24 + 27 + 28 + 22 + 24 )

=
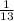`(1)/(13)`( 363

sample mean
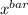`x^(bar)` = 27.9231

next we find the standard deviation

s = √(
`(1)/(n-1)`∑(
`x_(i)-x^(bar)`)²

x (
`x_(i)-x^(bar)`) (
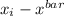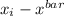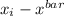`x_(i)-x^(bar)`)²

27 -0.9231 0.8521

41 13.0769 171.0053

22 -5.9231 35.0831

27 -0.9231 0.8521

23 -4.9231 24.2369

35 7.0769 50.0825

30 2.0769 4.3135

33 5.0769 25.7749

24 -3.9231 15.3907

27 -0.9231 0.8521

28 0.0769 0.0059

22 -5.9231 35.0831

24 -3.9231 15.3907

sum 378.9229

so ∑(
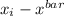`x_(i)-x^(bar)`)² = 378.9229

∴

s = √(
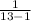`(1)/(13-1)` ×378.9229 )

s = √31.5769

standard deviation s = 5.6193

now, the Test statistics

t = (
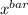`x^(bar)` - μ ) /
`(s)/(√(n) )`

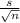
we substitute

t = ( 27.9231 - 25 ) /
`(5.6193)/(√(13) )`

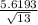
t = 2.9231 / 1.5585

t = 1.88

now degree of freedom df = n - 1 = 13 - 1 = 12

next we calculate p-value

p-value = 0.042299 ( using Execl's ( = TDIST(1.88,12,1)))

Here x=1.88, df=12, one tail

now we compare the p-value with the level of significance

since p-value (0.042299) is lesser than the level of significance ( 0.05)

We Reject Null Hypothesis

Hence, There is no sufficient evidence that the true average activation time is at most 25 seconds