Question

Verify the identity. cos^(2)xˢᵉᶜ²x+ᵗᵃⁿ²)x=ˢᵉᶜ²x

Answer 1

Yes, the given trigonometric identity is true:
`\( \cos^2(x) \sec^2(x) + \tan^2(x) = \sec^2(x) \).`

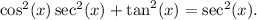
Step-by-step explanation:

The given trigonometric identity involves various trigonometric functions. Let's break down the proof step by step.

Firstly, rewrite the expression using the definitions of secant and tangent:

`\[ \cos^2(x) \sec^2(x) + \tan^2(x) = \cos^2(x) \left((1)/(\cos^2(x))\right) + (\sin^2(x))/(\cos^2(x)) \]`

Simplify the expression by canceling out common terms:

`\[ 1 + \tan^2(x) = \sec^2(x) \]`

Now, recall the fundamental trigonometric identity
`\(1 + \tan^2(x) = \sec^2(x)\)`, which confirms the given identity. Therefore, the original expression equals
`\(\sec^2(x)\)`, proving the identity.

In summary, by manipulating the given expression using trigonometric definitions and known identities, we arrive at the conclusion that
`\( \cos^2(x) \sec^2(x) + \tan^2(x) \) indeed equals \( \sec^2(x) \)`, verifying the identity.