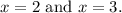Final Answer
The vertical asymptotes of the function
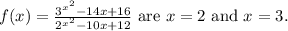
Step-by-step explanation
Vertical asymptotes occur when the denominator of a rational function equals zero, leading to undefined values. To find these points for f(x) , set the denominator
 equal to zero and solve for x . Factoring the quadratic expression yields
equal to zero and solve for x . Factoring the quadratic expression yields
 . Setting each factor equal to zero gives
. Setting each factor equal to zero gives
 Solving these equations, we find
Solving these equations, we find
 s the values at which the denominator becomes zero.
s the values at which the denominator becomes zero.
Now, let's consider the explanation for these results. When \x = 3 , the denominator becomes
 . Similarly, when x = 2 , the denominator becomes
. Similarly, when x = 2 , the denominator becomes
 In both cases, the denominator equals zero, indicating vertical asymptotes at
In both cases, the denominator equals zero, indicating vertical asymptotes at
 approaches these values, the function f(x) tends toward positive or negative infinity, signifying the presence of vertical asymptotes at these points. Thus, the identified vertical asymptotes for the given function are
approaches these values, the function f(x) tends toward positive or negative infinity, signifying the presence of vertical asymptotes at these points. Thus, the identified vertical asymptotes for the given function are