Question

ABCD- parallelogram, If the perimeter of Triangle CPQ is 15cm, Find the perimeter of triangle BAQ. Find the perimeter of triangle PDA. PLEASE FIND THE ANSWER QUICKLY I NEED IT RIGHT NOW

Answer 1

The answer is below

Explanation:

A parallelogram is a quadrilateral (has 4 sides and 4 angle) with two pair of parallel and opposite sides. Opposite sides of a parallelogram are parallel and equal.

Given parallelogram ABCD:

AB = CD = 18 cm; BC = AD = 8 cm

∠P = ∠P, ∠PDA = ∠PCQ (corresponding angles are equal).

Hence ΔPCQ and ΔPDA are similar by angle-angle similarity theorem. For similar triangles, the ratio of their corresponding sides equal. Therefore:

`(CD)/(PC)= (AD)/(CQ)\\\\(18)/(6)=(8)/(x) \\\\x=(6*8)/(18)=(8)/(3)\ cm`

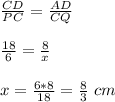
Perimeter of CPQ = CP + CQ + PQ

15 = 6 + 8/3 + PQ

PQ = 15 - (6 + 8/3)

PQ = 6.33

∠CQP = ∠AQB (vertical angles), ∠QCP = ∠QBA (alternate angles are equal).

Hence ΔCPQ and ΔABQ are similar by angle-angle similarity theorem

`(AQ)/(QP)=(AB)/(CP) \\\\(AQ)/(6.33) =(18)/(6) \\\\AQ=(18)/(6)*6.33\\\\AQ = 19`

`(BQ)/(CQ)=(AB)/(CP) \\\\(BQ)/(8/3) =(18)/(6) \\\\BQ=(18)/(6)*(8)/(3) \\\\BQ =8`

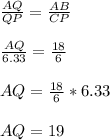
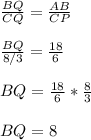
Perimeter of BAQ = AB + BQ + AQ = 18 + 8 + 19 = 45cm

PA = AQ + PQ = 19 + 6.33 = 25.33

PD = CD + DP = 18 + 6 = 24

Perimeter of PDA = PA + PD + AD = 24 + 25.33 + 8 = 57.33 cm