Question

Solve the equation, where 0 <= x < 360 tan x - 21.7 = 0

Answer 1

The equation is:

`\[ x = \tan^(-1)(21.7) \approx 87.13^\circ \]`

Step-by-step explanation:

The given equation is
`\( \tan x - 21.7 = 0 \), and we need to solve for \( x \)`where
`\( 0 \leq x < 360 \). To find \( x \),` we take the arctangent (inverse tangent) of both sides. This gives us
`\( x = \tan^(-1)(21.7) \)`. Evaluating this expression, we find
`\( x \approx 87.13^\circ \).`

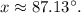
In the context of the unit circle, the inverse tangent represents the angle whose tangent is the given value. So,
`\( \tan^(-1)(21.7) \)` gives us the angle whose tangent is 21.7. In the specified range
`\( 0 \leq x < 360 \), \( x \approx 87.13^\circ \)` is the solution to the equation. This means that the tangent of
`\( 87.13^\circ \)` is approximately 21.7, satisfying the given equation.

It's important to note that trigonometric functions have periodic behavior, so there could be multiple solutions. However, in this case, we consider the solution within the specified range \( 0 \leq x < 360 \). The arctangent function provides a unique solution in this range, making \( x \approx 87.13^\circ \) the valid and final answer.