Question

​​​​​​​f(x)=5sin(2x)(1-x)(Use symbolic notation and fractions where needed.)f(x)=

Answer 1

The function
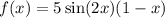`\(f(x) = 5\sin(2x)(1-x)\)` is a composite function that combines three elements: a constant multiplier (5), a sine function with double the argument
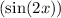`(\(\sin(2x)\))`, and a linear term
`\((1-x)\)`. The constant multiplier influences the amplitude of the function, the sine function introduces oscillations, and the linear term contributes a linear decrease as
`\(x\)`increases.

Step-by-step explanation:

In breaking down the components of the function, the constant term 5 acts as a multiplier, scaling the overall amplitude of the function. The sine function
`\(\sin(2x)\)` introduces periodic oscillations due to its nature, causing the function to fluctuate between positive and negative values as
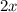`\(2x\)`varies. The linear term
`\((1-x)\)` contributes a linear decrease as
`\(x\)`increases, affecting the overall trend of the function.

Multiplying these terms together forms the complete function
`\(f(x)\)`, and each component plays a crucial role in shaping its behavior. Understanding the properties of the sine function, the impact of the linear term, and the influence of the constant allows for a comprehensive analysis of how the function behaves for different values of
`\(x\)`.

In essence,
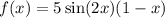`\(f(x) = 5\sin(2x)(1-x)\)` represents a nuanced interplay of mathematical elements, where the combination of a constant, a sine function, and a linear term results in a function with distinct oscillatory and decreasing characteristics. This breakdown aids in interpreting the function's behavior and exploring its properties within mathematical contexts.