Question

Plot all of the existing five features of the following rational function (some may not be needed). if you get a fraction or decimal then plot as close to the true location as possible. f(x)=x2+3x-10/2x2-11x=14

Answer 1

The features of the rational function plotted on the graph is added as an attachment

Plotting all of the features of the rational function

From the question, we have the following parameters that can be used in our computation:

`\text{f(x)} = (x^2 + 3x - 10)/(2x^2 - 11x + 14)`

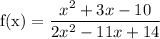
Factorize the numerator and the denominator

So, we have

`\text{f(x)} = ((x + 5)(x - 2))/((2x - 7)(x - 2))`

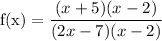
Cancel out the common factors

`\text{f(x)} = (x + 5)/(2x - 7)`

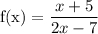
Set the cancelled factor to 0

So, we have

x - 2 = 0

x = 2

This means that the function has a hole at x = 2

Next, we set the denominator to 0 for the vertical asymptote

2x - 7 = 0

2x = 7

x = 3.5

This means that the function has a vertical asymptote at x = 3.5 and a domain at x ≠ 3.5

The domain is then expressed as (-∝, 3.5) U (3.5, ∝)

For the horizontal asymptote, we have

y = 1/2 --- where 1 and 2 are the leading coefficients of the numerator and the denominator of the function

This means that the function has a horizontal asymptote at y = 0.5 and a range at (-∝, 0.5) U (0.5, ∝)

The graph is attached