Question

A rational expression whose numerator, denominator, or both contain one or more rational expressions is called a BLANK.

Answer 1

A rational expression whose numerator, denominator, or both contain one or more rational expressions is called a complex fraction.

Step-by-step explanation:

In mathematics, a complex fraction is defined as a fraction where the numerator, denominator, or both contain one or more rational expressions. Rational expressions are ratios of polynomials, and when they appear in either the numerator or denominator of a fraction, the expression is termed "complex." To better understand this, consider an example:

`\[ (2x)/(3x^2 + 1) \]`

Here, the numerator
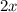`\(2x\)` and the denominator
`\(3x^2 + 1\)` are both rational expressions. Therefore, this fraction is a complex fraction. Complex fractions often involve multiple levels of fractions, creating a more intricate mathematical structure. They are a crucial concept in algebra, particularly when simplifying expressions or solving equations involving rational functions.

To simplify a complex fraction, one typically finds a common denominator and combines the fractions into a single fraction. For instance, if dealing with the complex fraction
`\(((a)/(b))/((c)/(d))\)`, you can multiply the numerator and denominator of the overall fraction by
`\(bd\)` to eliminate the inner fractions and simplify the expression.

Understanding complex fractions is essential in various mathematical applications, including calculus, where they often arise in problems involving limits, derivatives, and integrals. Mastery of this concept enhances a student's ability to manipulate algebraic expressions and solve more advanced mathematical problems.

Answer 2

A rational expression whose numerator, denominator, or both contain one or more rational expressions is called a "compound rational expression."

Step-by-step explanation:

In mathematics, a rational expression is a fraction in which both the numerator and denominator are polynomials. When either the numerator, denominator, or both in a rational expression contain one or more rational expressions, it is termed a "compound rational expression." Compound rational expressions can involve various operations such as addition, subtraction, multiplication, and division of rational expressions within the numerator, denominator, or both.

For example, consider the compound rational expression
`\((2x)/(x^2 + 1) + (3)/(2x - 1)\)`. In this expression, both the numerator and the denominator contain rational expressions. The terms
`\(2x\) and \(x^2 + 1\)` in the first fraction, as well as
`\(3\)`and
`\(2x - 1\)` in the second fraction, are all rational expressions. Combining them in a single expression with addition makes it a compound rational expression.

Understanding compound rational expressions is crucial in algebraic manipulation, simplification, and solving equations involving fractions. The rules for operating on rational expressions extend to compound rational expressions, allowing mathematicians to work with more complex algebraic structures efficiently.