Answer:
a) h = 53.8 m, b) h_minimum = 28 m, h_maximum = 63.3 m
Step-by-step explanation:
a) For this exercise let's use Bernoulli's equation.
The subscript 1 is for the tank and the subscript for the building
P₁ + ½ ρ g v₁² + ρ g y₁ = P₂ + ½ ρ g v₂² + ρ g y₂
In general, the water tanks are open to the atmosphere, so P1 = Patm, also the tanks are very large so the speed of the water surface is very small v₁=0 and as they give us the precious static, this it is when the keys are closed so the output velocity is zero, v₂= 0. The height of the floors in a building is y₂ = 12 m
we substitute in Bernoulli's equation
P_{atm} + 0 + ρ g h = P₂ + 0 + ρ g y₂
h =
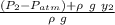
h =
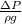 + y₂
+ y₂
indicate that the value of ΔP = 410 10³ Pa
we calculate
h = 410 10³ / (1000 9.8) + 12
h = 53.8 m
b) ask for the height range for the minimum and maximum pressure
h =
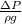 ΔP / rho g
ΔP / rho g
minimum
h_minimum = 275 103/1000 9.8
h_minimum = 28 m
maximums
h_maximo = 620 103/1000 9.8
h_maximum = 63.3 m