A graph of the constraint region is shown in the image below.
The minimum value of the objective function is 10.
In this exercise, we would graph the feasible region that is defined by the constraints and then, we would evaluate the objective function (z) at these vertices of the feasible region in order to find the minimum value.
Based on the points where the shaded regions overlap in the graph, we have the following vertices of the feasible region:
(3.5, 1.25), (6, 0), and (0, 10).
Now, we can evaluate the objective function C = 3x + y at these vertices as follows:
For (3.5, 1.25)
C = 3(3.5) + 1.25
C = 11.75.
For (6, 0)
C = 3(6) + 0
C = 18
For (0, 10)
C = 3(0) + 10
C = 10
In conclusion, the minimum value of the objective function is 10 while the maximum value of the objective function is 18.
Complete Question:
Solve the following using graphing techniques:
1.Minimize
 subject to the constraints,
subject to the constraints,
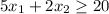
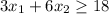
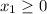
 .
.