Question

Suppose you deposit a lump-sum of $15,000 in an account that earns 7.5% interest compounded monthly. How much would be in the account after a term of 12 years? b. Suppose you deposit a lump-sum of $15,000 in an account that earns 7.5% interest compounded continuously. How much would be in the account after a term of 12 years?

Answer 1

To determine the final amount in an account after 12 years with a $15,000 initial deposit at 7.5% interest, different calculations are done for monthly compounding and continuous compounding. The compounded monthly amount is approximately $30,598.31, while the continuously compounded amount is approximately $36,894.05.

Step-by-step explanation:

To calculate the final amount in an account after a term of 12 years with an initial deposit of $15,000 at 7.5% interest compounded monthly, we use the compound interest formula:

`A = P(1 + rac{r}{n})^(nt).`

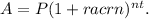
Here, P is the principal amount ($15,000), r is the annual interest rate (0.075), n is the number of times interest is compounded per year (12 for monthly), and t is the number of years (12).

For monthly compounding, the calculation is:

`A = 15000(1 + rac{0.075}{12})^(12*12).`

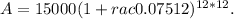
Similarly, for continuously compounded interest, we use the formula:

`A = Pe^(rt)`

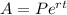
where e is the base of the natural logarithm, approximately equal to 2.71828. The calculation is:

`A = 15000e^(0.075*12).`

Let's compute each.

1. For monthly compounding:
   
2. 
   `A = 15000(1 + rac{0.075}{12})^(144) = 15000(1.00625)^(144) = 15000(2.0398873...) ≈ $30,598.31.`
3. For continuous compounding:
   
4. 
   `A = 15000e^(0.9) = 15000(2.4596031...) ≈ $36,894.05.`

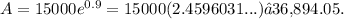
After 12 years, the account would have approximately $30,598.31 with monthly compounding, and approximately $36,894.05 with continuous compounding.