Question

Given a geometric sequence where a_(3)=320 and a_(6)=20480, find a_(8)

Answer 1

In a geometric sequence,
`\(a_n = a_1 * r^((n-1))\) where \(a_n\)` is the nth term,
`\(a_1\)` is the first term, r is the common ratio, and n is the term number. By the help of this geometric sequence
`\(a_8 = 327680\)`.

Step-by-step explanation:

We're given that
`\(a_3 = 320\) and \(a_6 = 20480\)` in the geometric sequence. Using the formula
`\(a_n = a_1 * r^((n-1))\)`, we can form two equations:

1. For
`\(n = 3\): \(a_3 = a_1 * r^((3-1)) = a_1 * r^2 = 320\)`

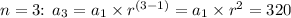
2. For
`\(n = 6\): \(a_6 = a_1 * r^((6-1)) = a_1 * r^5 = 20480\)`

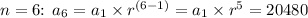
Divide the second equation by the first to eliminate
`\(a_1\)`:

`\((a_6)/(a_3) = (a_1 * r^5)/(a_1 * r^2) = r^3 = (20480)/(320) = 64\)`

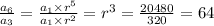
Now that we've found the common ratio
`(\(r^3 = 64\))`, we can find r by taking the cube root:
`\(r = \sqrt[3]{64} = 4\)`.

Next, we need to find
`\(a_1\)`, the first term. We can use
`\(a_3 = 320\)` to find it:

`\(a_3 = a_1 * r^((3-1)) = a_1 * 4^2 = 320\)`

`\(a_1 * 16 = 320\)`

`\(a_1 = (320)/(16) = 20\)`

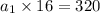
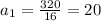
Finally, to find
`\(a_8\)`, substitute the values into the formula:

`\(a_8 = a_1 * r^((8-1)) = 20 * 4^7 = 20 * 16384 = 327680\)`

Therefore,
`\(a_8 = 327680\)` in the geometric sequence.