Final answer:
The parabola represented by the equation
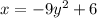
opens to the left because the coefficient of the
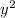
term is negative.
Step-by-step explanation:
The equation you've provided,
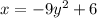
, represents a parabola. To determine which direction this parabola opens, look at the coefficient of the
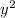
term. In this case, the coefficient is -9, which is negative. This means that the parabola opens to the left if you're looking at a standard graph with x and y axes. In the standard orientation, parabolas that are functions of y² open either left or right depending on the sign of the coefficient before the y² term. If the coefficient is negative as it is in this case, the parabola opens to the left. If it were positive, the parabola would open to the right.