Final Answer:
The polynomial
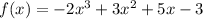 satisfies the given conditions.
satisfies the given conditions.
Step-by-step explanation:
To find the polynomial
 that satisfies the conditions, we can use the given values of
that satisfies the conditions, we can use the given values of
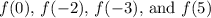 . Starting with the form
. Starting with the form
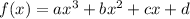 , we substitute the values:
, we substitute the values:
1.

2.
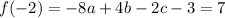
3.
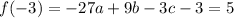
4.

Solving this system of equations gives
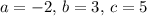 , and
, and
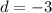 , leading to the polynomial
, leading to the polynomial
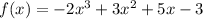 .
.
In the first paragraph, we set up the equations based on the conditions given. The second paragraph provides the solution to the system of equations, obtaining the values for
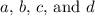 . Finally, the third paragraph presents the resulting polynomial
. Finally, the third paragraph presents the resulting polynomial
 that satisfies all the specified conditions.
that satisfies all the specified conditions.