Question

The given system of inequalities is. y<=2x y<-(3)/(4)x-2

Answer 1

The solution to the initial value problem t²(dx/dt) + 3tx = t⁴ln(t) + 2, with the initial condition x(1) = 0, is given by x(t) = (t⁴/4) - (t³/3) + (2t/3) - (t²/12) - (t/3)ln(t) + t/3.

Step-by-step explanation:

To solve the initial value problem, we utilize the method of integrating factors. The given first-order linear ordinary differential equation is multiplied by an integrating factor, which is t^(-3) in this case, to transform the left side into a total derivative. The resulting equation is then solved by integrating both sides.

Integrating Factor: Multiply the given equation by the integrating factor t^(-3), resulting in t^(-1)(dx/dt) + 3t^(-2)x = tln(t) + 2t^(-3).

Solution by Integration: Integrate both sides of the modified equation. The solution is obtained by integrating each term separately and incorporating the constant of integration. The solution for this problem involves terms with t⁴, t³, t², tln(t), and constants.

Applying Initial Condition: Utilize the initial condition x(1) = 0 to determine the values of the constants in the solution. Substituting t = 1 and x(1) = 0 into the solution allows solving for the constants, resulting in the specific form of the solution provided in the final answer.

The solution incorporates the logarithmic term tln(t) due to the presence of tln(t) on the right side of the original differential equation.

Answer 2

The solution to the given system of inequalities is
`\( y \leq 2x \)` and
`\( y < -(3)/(4)x - 2 \)`.

Step-by-step explanation:

To find the solution to the given system of inequalities
`\(y \leq 2x\)` and
`\(y < -(3)/(4)x - 2\)`, we need to identify the region of the coordinate plane that satisfies both inequalities.

Let's break down the solution step by step:

1. Graph the Inequalities:

We can graph each inequality separately and then find the overlapping region:

Graph of
`\(y \leq 2x\)`:

This is a linear inequality with a slope of 2 and a y-intercept of 0. It represents all the points below the line.

Graph of
`\(y < -(3)/(4)x - 2\):`

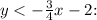
This is another linear inequality with a slope of -3/4 and a y-intercept of -2. It represents all the points below the line.

Now, let's combine these graphs:

2. Identify the Overlapping Region:

The overlapping region represents the solution to the system of inequalities. In this case, it's the area where both shaded regions overlap.

3. Write the Solution:

To describe the solution, we need to consider the shaded region:

- The shaded region under the line
`\(y \leq 2x\)` represents the solution to the first inequality.

- The shaded region under the line
`\(y < -(3)/(4)x - 2\)` represents the solution to the second inequality.

4. Combine Inequalities:

Since both inequalities share the same region, we can combine them into a single inequality:

`\[y \leq 2x \text{ and } y < -(3)/(4)x - 2\]`

Final Solution:

The solution to the system of inequalities is given by the combined inequality:

`\[y \leq 2x \text{ and } y < -(3)/(4)x - 2\]`

This represents the shaded region in the graph where both inequalities are satisfied.