Question

Evaluate the exponential funo y=16^(x) for x=-(3)/(4)

Answer 1

To evaluate the exponential function

`y=16^x for x=-3/4,`

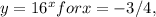
it can be rewritten using the base of

`2 (16=2^4)`

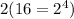
and evaluated as

`y=2^(-3),`

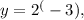
which simplifies to y=1/8.

Step-by-step explanation:

To evaluate the exponential function y=16x for x=-3/4, we first recognize that the exponential function can be expressed in terms of 2's powers since 16 is a power of 2 (specifically, 16 = 24). This allows us to rewrite the function as y=(24)x. Applying the exponent rule (ab)c = ab*c, the function becomes y=24x.

Substituting x with -3/4, we get: y=24*(-3/4) = 2-3 since the 4's cancel out. We can then evaluate 2-3 which is the inverse of 23 or 1/23. Finally, computing 23 gives us 8, so the inverse is 1/8.

Therefore, y = 1/8 when x = -3/4 for the exponential function y = 16x.