Question

Find the area between the curves. x=−5,x=2,y=7x,y=x²−8

Answer 1

The area between the curves is 83.33 square units.

Step-by-step explanation:

To find the area between the curves, we need to set up and evaluate the definite integral of the difference between the upper and lower curves with respect to x. The limits of integration are determined by the points of intersection of the curves. The curves y = 7x and
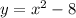`\(y = x^2 - 8\)`intersect at
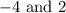`\(-4\) and \(2\)`. Therefore, the integral is set up as follows:

`\[ \int_(-5)^(2) [(x^2 - 8) - 7x] \,dx \]`

Solving this integral gives the area between the curves. The antiderivative is
`\((1)/(3)x^3 - (7)/(2)x^2 - 8x\)`, and when evaluated from
`\(-5\) to \(2\), the result is \(83.33\).`

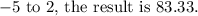
In this calculation, the upper curve is
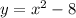`\(y = x^2 - 8\)` and the lower curve is
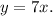`\(y = 7x\).` The subtraction in the integrand ensures that we are finding the area between these curves. The result represents the total area enclosed by the curves within the given interval.