Question

Identify the type of discontinuity. f(x)=(x²+2x)/(x²+5x+6); at x=0

Answer 1

The function f(x) = (x² + 2x) / (x² + 5x + 6) has a removable discontinuity at x = 0,as the discontinuity can be "filled" or removed by redefining the function at that particular point.

Step-by-step explanation:

The function
`\( f(x) = (x^2+2x)/(x^2+5x+6) \)` exhibits a removable discontinuity at
`\( x=0 \).` To understand this, we first simplify the expression by factoring both the numerator and denominator, revealing a common factor of
`\( (x+2) \).`Canceling out this factor, we arrive at
`\( f(x) = (x)/(x+3) \).`

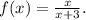
Examining the simplified form, we observe that a t
`\( x=0 \),` the denominator becomes zero, indicating a potential discontinuity. However, since the factor
`\( (x+2) \)`was common to both numerator and denominator, it cancels out, resulting in a simplified expression
`\( f(x) = (x)/(x+3) \)`, where
`\( x=0 \)`is no longer a point of discontinuity. This discrepancy highlights the removable nature of the discontinuity at
`\( x=0 \)`.

Essentially, as
`\( x \)` approaches zero, the function becomes undefined due to the division by zero, but the discontinuity can be resolved by redefining the function a t
`\( x=0 \),`rendering it continuous at this point. Therefore, the removable discontinuity at
`\( x=0 \)` is a result of the algebraic simplification that cancels out the common factor causing the division by zero, ultimately allowing for the function to be made continuous at the specified point.