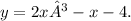Final Answer:
The correct parametrization of the graph of
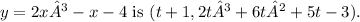
Step-by-step explanation:
The given parametrization
 can be used to express
can be used to express
 By substituting
By substituting
 we can verify its correctness.
we can verify its correctness.
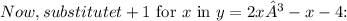
![\[y = 2(t + 1)³ - (t + 1) - 4\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qhhqaw90excb4udsbb8umvbn9rwiohaw3u.png)
Expand and simplify:
![\[y = 2(t³ + 3t² + 3t + 1) - t - 1 - 4\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/d3r6qjnyvkqq00o24t20knq5krbxoo024e.png)
![\[y = 2t³ + 6t² + 5t - 3\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wlzeqi21qbh1scwlkj7egcyn989pj1pd4n.png)
Thus, the expression matches the original function
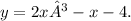 This confirms that the parametrization
This confirms that the parametrization
 correctly represents the graph of
correctly represents the graph of