Question

If x^2/16 + y^2/64 = 1 and y(3) = 2√7, find y'(3).

Answer 1

To find y'(3) for the ellipse equation

`x^2/16 + y^2/64 = 1 given that y(3) = 2√7`

, we implicitly differentiate and solve for y'. The answer is y'(3) = -3/(4√7).

Step-by-step explanation:

The equation

`x^2/16 + y^2/64 = 1`

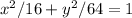
represents an ellipse. To find y'(3), we need to implicitly differentiate the given equation with respect to x. Let's perform the differentiation:

Differentiate both sides with respect to x: 2x/16 + 2yy'/64 = 0.

1. Simplify and solve for y': y' = -x/(2y).
2. Substitute x = 3 and y = 2√7 into the equation for y': y'(3) = -3/(4√7).

The value of y' at x = 3 is -3/(4√7).