Final answer:
The greatest common factor of
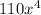
7, and 60x^9 is 10x^4, found by identifying the GCF of the numerical coefficients (which is 10) and taking the lowest exponent for x, which is 4.
Step-by-step explanation:
To find the greatest common factor (GCF) of the expressions 110x^4, 70x^7, and 60x^9, we will first factor out the numerical coefficients and then the variables separately.
The numerical coefficients of the given expressions are 110, 70, and 60. To find the GCF of these numbers, we can list their factors:
- 110: 1, 2, 5, 10, 11, 22, 55, 110
- 70: 1, 2, 5, 7, 10, 14, 35, 70
- 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
The common factors are 1, 2, 5, and 10. The greatest of these is 10.
Next, we look at the variable part. Since all expressions are powers of x, we take the lowest exponent of x, which is 4. So, x^4 is the greatest common factor of the variable part.
Therefore, the greatest common factor of 110x^4, 70x^7, and 60x^9 is 10x^4.