Question

Power and quotient rules with negative Simplify. ((3z)/(2z^(-5)))^(2) Write your answer using only positive exponents

Answer 1

The simplified expression with positive exponents is
`\((9z^(12))/(4)\)`.

Step-by-step explanation:

Sure, let's break this down step by step.

The expression is:
`\(\left((3z)/(2z^(-5))\right)^2\)`

Firstly, let's simplify the fraction inside the parentheses using the quotient rule of exponents:
`\(z^(m)/z^(n) = z^(m-n)\)`.

`\((3z)/(2z^(-5))\)` can be rewritten as
`\((3z \cdot z^5)/(2)\)` since
`\(z^(-5)\)` in the denominator moves to the numerator as \(z^5\) (changing the sign of the exponent).

Now the expression becomes:
`\(\left((3z \cdot z^5)/(2)\right)^2\)`

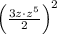
Next, simplify within the parentheses:
`\(3z \cdot z^5 = 3z^6\)` (when multiplying variables with the same base, you add the exponents).

Now, the expression becomes:
`\(\left((3z^6)/(2)\right)^2\)`

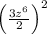
Finally, apply the power rule of exponents:
`\((a/b)^n = a^n/b^n\).`

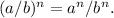
So,
`\(\left((3z^6)/(2)\right)^2 = ((3z^6)^2)/(2^2) = (9z^(12))/(4)\).`