Question

Use linear approximation to approximate sqrt(64.4) as follows. Let (x)=√x. The equation of the tangent line to (x) at x=64 can be written in the form y=mx+.

Compute m and .

m=
=

Using this find the approximation for √64.4.

Answer 1

The linear approximation for √(64.4) using the tangent line at
`\(x=64\)` is approximately
`\(8.02\).`

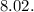
Step-by-step explanation:

To find the linear approximation, we first need to compute the slope m and the y-intercept b for the tangent line at
`\(x=64\).`

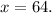
The slope
`\(m\)` is the derivative of
`\(y(x)\)`evaluated at
`\(x=64\), which is \(1/(2√64) = 1/16\).`

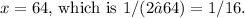
The y-intercept
`\(b\) is \(y(64) - m * 64\),`

where
`\(y(64) = √64 = 8\). Therefore, \(b = 8 - (1/16) * 64 = 4\)`.

Hence, the equation of the tangent line is
`\(y = (1/16)x + 4\)`.

To approximate √(64.4), we plug in
`\(x=64.4\)` into the equation of the tangent line:

`\[y ≈ (1/16) * 64.4 + 4\]`

`\[y ≈ 4.025 + 4\]`

`\[y ≈ 8.025\]`

Therefore, the linear approximation for √(64.4) is approximately
`\(8.02\)`. This method is a useful approximation when dealing with small changes in a function and provides a close estimate without the need for complex calculations.