Question

What value of a complotes the oquation y=a*2^(x) for the exponertial growth function shown?

Answer 1

The value of (a) that completes the equation
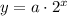`\(y = a \cdot 2^x\)` for the exponential growth function is
`\(a = y \cdot 2^(-x)\).`

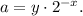
Step-by-step explanation:

In the given exponential growth function
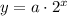`\(y = a \cdot 2^x\)`, (a) represents the initial value or the y-intercept, and
`\(2^x\)` represents the exponential growth factor. To find the value of (a), we can rearrange the equation to isolate (a). Dividing both sides of the equation by
`\(2^x\)`, we get
`\(a = y \cdot 2^(-x)\)`.

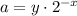This result makes sense intuitively because dividing by
`\(2^x\)` essentially "cancels out" the exponential growth factor, leaving us with the initial value (a). It is important to note that this formula for (a) allows us to determine the starting point of the exponential growth process when the values of (y) and (x) are known.

For example, if we have a specific point (x, y) on the curve, we can substitute these values into the equation
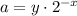`\(a = y \cdot 2^(-x)\)` to find the corresponding initial value (a). This is a useful tool in understanding and analyzing exponential growth functions, particularly in scenarios such as population growth, financial investments, or biological processes.