Question

Write an equation in slope-intercept form of the line shown. (3,1) (1,-3)​

Answer 1

`y = 2x - 5`

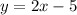
Explanation:

The first step in finding the equation of a line from a given set of points is to find its slope. The slope of a line is defined by the formula:

`m = \frac{\textrm{rise}}{\textrm{run}} = (y_2 - y_1)/(x_2 - x_1)`

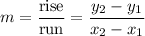
In this problem, we are given two points in the form
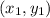`(x_1, y_1)` and
`(x_2, y_2)`.

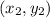So, we can define the x's and y's as:

`x_1 = 3`,
`y_1 = 1`,
`x_2 = 1`,
`y_2 = -3`.

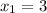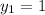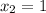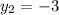Hence, the slope of the line can be solved for.

`m = (-3 - 1)/(1 - 3)`

`m=(-4)/(-2)`

`m = 2`

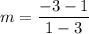
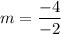
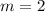
So, the slope of the line is 2.

Now, we can plug this into the point-slope equation for a line where (a, b) is a point on the line and m is its slope.

`y - b = m(x - a)`

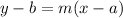
I will use the point (3, 1):

`y - 1 = 2(x - 3)`

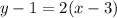
and isolate y to put it into slope-intercept form.

`y - 1 = 2x - 6`

`y = 2x - 6 + 1`

`y = 2x - 5`

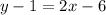
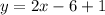
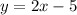
So, the equation in slope-intercept form for the line that goes through the points (3, 1) and (1, -3) is
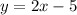`y = 2x - 5`.