Answer:
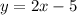
Explanation:
The first step in finding the equation of a line from a given set of points is to find its slope. The slope of a line is defined by the formula:
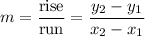
In this problem, we are given two points in the form
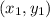 and
and
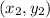 .
.
So, we can define the x's and y's as:
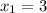 ,
,
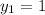 ,
,
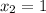 ,
,
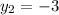 .
.
Hence, the slope of the line can be solved for.
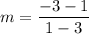
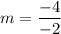
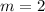
So, the slope of the line is 2.
Now, we can plug this into the point-slope equation for a line where (a, b) is a point on the line and m is its slope.

I will use the point (3, 1):

and isolate y to put it into slope-intercept form.
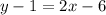
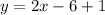
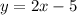
So, the equation in slope-intercept form for the line that goes through the points (3, 1) and (1, -3) is
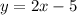 .
.