Question

Approximation of R(51) using information from R′(x):

Given the options, if you want to approximate R(51) using the derivative R′(x), you'd use the concept of a linear approximation or differential, which states:
R(51)≈R(50)+R′(50)×(51−50)

Answer 1

To approximate R(51) using information from R′(x) , the linear approximation formula is employed:
`\( R(51) \approx R(50) + R′(50) * (51 - 50) \).`

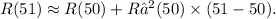
Step-by-step explanation:

The concept of linear approximation, also known as differentials, allows us to estimate the value of a function at a point using information from its derivative. In this case, to approximate ( R(51) , we use the formula ( R(51) \approx R(50) + R′(50) \times (51 - 50) . This formula is derived from the linearization of the function at a nearby point, in this instance, ( x = 50 ). The term ( R′(50) \times (51 - 50) represents the linear approximation, providing an estimate based on the rate of change of the function at \( x = 50 \).

In the given expression, ( R(50) ) corresponds to the known value of the function at ( x = 50 ), and ( R′(50) ) represents the derivative of ( R(x) ) evaluated at \( x = 50 \). Multiplying the derivative by the change in ( x ) from the approximation point yields an estimate for the change in the function value. Adding this to the known value ( R(50) ) provides an approximation for ( R(51) ). This technique is particularly useful when precise values are challenging to obtain, and a linear approximation provides a reasonable estimate.