Question

A price p (in dollars) and demand x for a product are related by

2 x²-2 x p+50 p²=13400
If the price is increasing at a rate of 2 dollars per month when the price is 10 dollars, find the rate of change of the demand.

Answer 1

When the price is increasing at $2 per month and the price is $10, the rate of change of demand is approximately 8.77 units per month.

How to find rate of change of the demand

Given:

Equation:
`2x^2 - 2xp + 50p^2 = 13400`

Price is increasing at a rate of $2 per month (dp/dt = 2).

Price is $10 (p = 10).

Substitute p = 10 into the equation to find x:

`2x^2 - 2x * 10 + 50 * 10^2 = 13400\\2x^2 - 20x + 5000 = 13400\\2x^2 - 20x = 13400 - 5000\\2x^2 - 20x = 8400`

Rearrange the equation:

`2x^2 - 20x - 8400 = 0`

Solve for x using the quadratic formula:

x = (-b ± √(
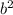`b^2` - 4ac)) / 2a

Here, a = 2, b = -20, c = -8400

Calculate the discriminant:

Discriminant (D) =
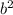`b^2` - 4ac

D =
`(-20)^2` - 4 * 2 * (-8400)

D = 400 + 67200

D = 67600

Solve for x using the quadratic formula:

x = (20 ± √67600) / 4

x = (20 ± 260) / 4

Calculate the roots:

x = (20 + 260) / 4 = 280 / 4 = 70 (using the positive root)

Therefore, when the price is $10, the demand x is 70.

Now, find the rate of change of demand (dx/dt) when the price is increasing at $2 per month:

Using the equation:
`2x^2 - 2xp + 50p^2 = 13400`

Differentiate both sides with respect to time (t):

`d/dt(2x^2 - 2xp + 50p^2) = d/dt(13400)`

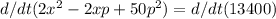
4x(dx/dt) - 2x(dp/dt) - 2p(dx/dt) + 100p(dp/dt) = 0

Substitute known values: p = 10, dp/dt = 2, x = 70 into the equation:

4(70)(dx/dt) - 2(70)(2) - 2(10)(dx/dt) + 100(10)(2) = 0

280(dx/dt) - 280 - 20(dx/dt) + 2000 = 0

260(dx/dt) = 2280

(dx/dt) = 2280 / 260

(dx/dt) = 8.77

Therefore, when the price is increasing at $2 per month and the price is $10, the rate of change of demand is approximately 8.77 units per month.