Question

Cos(x+b) sinx=(15)/(17) and is in quadrant I sinb=(4)/(5) and is in quadrant II

Answer 1

The solution to the trigonometric equation cos(x + b)sinx = 15/17, where sinb = 4/5, in quadrant I is x = arcsin(4/5), and in quadrant II is x = π - arcsin(4/5), with b = arcsin(4/5).

Step-by-step explanation:

We are given the equation cos(x + b)sinx = 15/17 and sinb = 4/5. To find the solution, we can use the double-angle identity for cosine, which is cos²(θ) = 1 - sin²(θ). Applying this identity, we get:

`\[2cos(x)cos(b)sin(x) = 15/17\]`

Rearranging, we have
`\[cos(x)cos(b) = (15)/(34sin(x)).\]`

Now, using the Pythagorean identity sin²(θ) + cos²(θ) = 1, we find that
`\(cos^2(b) = 1 - sin^2(b) = (9)/(25).\)`

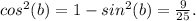
Substituting this into the previous equation and simplifying, we find
`\[cos(x) = (3)/(5).\]`

Now, we know sin(x) = 4/5 (given), and cos(x) = 3/5, so x = arcsin(4/5). Since sinb is positive, b is also in the first quadrant.

However, we are also asked to find a solution in quadrant II. In quadrant II,
`\[x = π - arcsin(4/5),\]` and b =
`\[π - arcsin(4/5).\]`