Final Answer:
To differentiate the function y = x
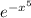 with respect to x, we'll use the product rule and chain rule. The derivative of y = x
with respect to x, we'll use the product rule and chain rule. The derivative of y = x
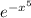 with respect to x is
with respect to x is
 - 5x⁵
- 5x⁵
 .
.
Step-by-step explanation:
To differentiate the function y = x
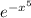 with respect to x, we'll use the product rule and chain rule.
with respect to x, we'll use the product rule and chain rule.
The product rule states that if u and v are functions of x, then the derivative of uv with respect to x is given by (uv)' = u'v + uv'.
Let u = x and v =
 . Then, we have:
. Then, we have:
y = u v
Now, apply the product rule:
y' = u'v + uv'
The derivative of u with respect to x is 1, and the derivative of v with respect to x involves the chain rule:
v' = -5x⁴
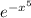
Now substitute these into the product rule formula:
y' = 1 ·
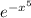 + x · (-5x⁴
+ x · (-5x⁴
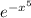 )
)
Simplify:
y' =
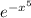 - 5x⁵
- 5x⁵
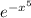
Therefore, the derivative of y = x
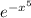 with respect to x is
with respect to x is
 - 5x⁵
- 5x⁵
 .
.