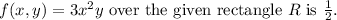Final answer:
the average value of
 over the given rectangle
over the given rectangle
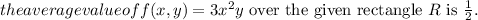
Step-by-step explanation:
To find the average value of the function
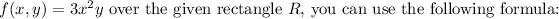
![\[ \text{Average value} = \frac{1}{\text{Area of } R} \iint_R f(x, y) \, dA \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5l6fuoe5adrzdxl0v4ji24d9933jvbye6h.png)
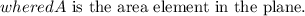
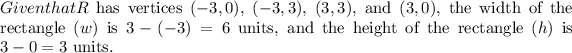
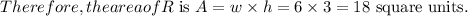
Now, you can set up the double integral to find the average value:
![\[ \text{Average value} = (1)/(18) \iint_R 3x^2y \, dA \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vao6lxwtmj3vlkhtum0lzr9vxsh8j6uujg.png)
To integrate over \(R\), you need to define the limits of integration. In this case, \(x\) ranges from \(-3\) to \(3\) and \(y\) ranges from \(0\) to \(3\).
![\[ \text{Average value} = (1)/(18) \int_(-3)^(3) \int_(0)^(3) 3x^2y \, dy \, dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/l4tpta777cujfwnon2msxk8x6ilf5wof7v.png)
Now, perform the integration:
![\[ \text{Average value} = (1)/(18) \int_(-3)^(3) \left[(3)/(2)x^2y^2\right]_(0)^(3) \, dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tb1kag49z79w00fg7q99ckylls0o7wskuj.png)
![\[ \text{Average value} = (1)/(18) \int_(-3)^(3) (27)/(2)x^2 \, dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9q87suftg2q9j0lcw5nfbrabmdubjexovq.png)
![\[ \text{Average value} = (1)/(18) \left[(9)/(2)x^3\right]_(-3)^(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ogm5ssry77uzezbgsgx3n6okgvhqpjpfyl.png)
![\[ \text{Average value} = (1)/(18) \left[(9)/(2)(27) - (9)/(2)(-27)\right] \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6nuiuojf1bwfe0zxu6sex8pme2lfamm0hn.png)
![\[ \text{Average value} = (1)/(18) * (9)/(2) * 54 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ldkms5j44znitahb48znb0z1o7nwtbsz0p.png)
![\[ \text{Average value} = (1)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rkt5p9oj71ecji5qiowcofr6fu4xr791gq.png)
So, the average value of