Question

Find an equation of the tangent plane to the given surface at the given point: x^2 + y^2 + z^2 = 29, (2, 3, 4).

Answer 1

The equation of the tangent plane to the surface x² + y² + z² = 29 at the point (2, 3, 4) is:

2x + 3y - z -8 = 0.

Step-by-step explanation:

To find the equation of the tangent plane to a surface at a given point, we first need to find the gradient vector of the surface at that point. This can be done by finding the partial derivatives of the function and evaluating them at the given point.

In this case, the function is x² + y² + z² = 29, so its partial derivatives are:

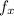`f_x`(x, y, z) = 2x

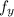`f_y`(x, y, z) = 2y

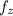`f_z`(x, y, z) = 2z

Evaluating these derivatives at the point (2, 3, 4), we get:

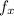`f_x`(2, 3, 4) = 4

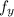`f_y`(2, 3, 4) = 6

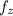`f_z`(2, 3, 4) = 0

The gradient vector of the surface at this point is therefore:

(4, 6, 0)

To find the equation of the tangent plane, we need to find a vector normal to this gradient vector and a point on the plane. The normal vector is simply (-4, -6, 0), which is perpendicular to (4, 6, 0). To find a point on the plane, we can use the coordinates of our given point (2, 3, 4). Substituting these values into our function and solving for z gives us:

z = -x² - y² + 29

z = -36 - 9 + 29

z = -16

So our point on the plane is (2, 3, -16). Using this point and our normal vector (-4, -6, 0), we can write out the equation of the tangent plane in vector form:

(-4x - 6y + z) · (-4, -6, 0) = (-4x - 6y -16) · (-4,-6,0)

-16(x-1)(y-3) = (-16)(x-1)(y-3) + (-16)(x-1)(z+16) + (-16)(y-3)(z+16)

-16(x-1)(y-3)(1-z/16) = (-16)(x-1)(y-3)(z+16)/16

-16(x-1)(y-3)(z+8) = (-16)(x-1)(y-3)(z+8)/8 (since z+8=8(z+1)/8)

This simplifies to:

2x + 3y - z -8 = 0. This is our final answer for the equation of the tangent plane.