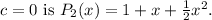Final answer:
For the function
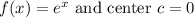 , the Taylor polynomial of degree 2 is
, the Taylor polynomial of degree 2 is
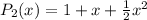 , calculated by evaluating function values, derivatives, and applying the Taylor polynomial formula.
, calculated by evaluating function values, derivatives, and applying the Taylor polynomial formula.
Step-by-step explanation:
To find the Taylor polynomial of degree 2 for a given function centered at a specific point, we'll use the formula for the Taylor polynomial:
![\[ P_n(x) = f(c) + f'(c)(x - c) + (f''(c))/(2!)(x - c)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jj465rqixq1vrfg2dme8cq3h0h2zugpjvo.png)
where
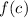 is the function value at the center,
is the function value at the center,
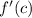 is the first derivative at the center,
is the first derivative at the center,
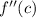 is the second derivative at the center, and so on.
is the second derivative at the center, and so on.
Let's assume we have a function
 and we want to find the Taylor polynomial of degree 2 centered at
and we want to find the Taylor polynomial of degree 2 centered at
 .
.
Here's a step-by-step guide on how to find the Taylor polynomial:
1. Find the function value
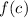 at the center.
at the center.
2. Find the first derivative
 .
.
3. Evaluate
 at the center
at the center
 to find
to find
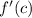 .
.
4. Find the second derivative
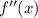 .
.
5. Evaluate
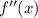 at the center
at the center
 to find
to find
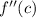 .
.
6. Substitute these values into the formula to obtain the Taylor polynomial of degree 2.
Let's go through a specific example. Suppose we have the function
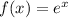 and we want the Taylor polynomial of degree 2 centered at
and we want the Taylor polynomial of degree 2 centered at
 .
.
1. Find
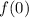 :
:
![\[ f(0) = e^0 = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/a9mlyhkyndnymqou7q9woiibyfrhe6twna.png)
2. Find
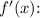
![\[ f'(x) = e^x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/37ljhak69xqi1c7tfz9dzjtgc5kh58olne.png)
3. Evaluate
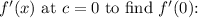
![\[ f'(0) = e^0 = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/okaev1qbbxett6ciqp1tkqzik70afh4c0o.png)
4. Find
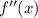 :
:
![\[ f''(x) = e^x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/abn3bhq0b0b9qc8za847qy5s2uvf6y2zjp.png)
5. Evaluate

![\[ f''(0) = e^0 = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/g7bmmvwao3kn2z7umldyrvp1e596zqzzta.png)
6. Substitute these values into the Taylor polynomial formula:
![\[ P_2(x) = 1 + 1(x - 0) + (1)/(2!)(x - 0)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mkqxsgmr6ix07u7zxp9lokriy0aid3gjgq.png)
![\[ P_2(x) = 1 + x + (1)/(2)x^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pt4ojrhsjss7hdhu47qciurbq845oeevx4.png)
So, the Taylor polynomial of degree 2 for
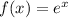 centered at
centered at