Question

The coordinate axes in the figure run through the centroid of a solid wedge parallel to the labeled edges. The wedge has a=8​, b=3​, and c=9. The solid has constant density δ=1.The square of the distance from a typical point​ (x,y,z) of the wedge to the line​ L: z=​0, y=3 is r2=(y−3)2+z2. Calculate the moment of inertia of the wedge about L.

Answer 1

The moment of inertia of the solid wedge about the line
`L: z=0, y=3 is \(I_L = (91)/(3)\).`

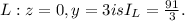
Step-by-step explanation:

To calculate the moment of inertia, we integrate the density function over the volume of the solid wedge. The density
`\(\delta\)`is constant, so we can use the expression for the moment of inertia about an axis parallel to the y-axis:

`\[I_y = \iiint_R r^2 \delta \, dV\]`

Given that
`\(r^2 = (y-3)^2 + z^2\)`, the volume element
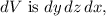`\(dV\) is \(dy \, dz \, dx\), \\`and the limits of integration are
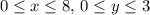`\(0 \leq x \leq 8\), \(0 \leq y \leq 3\)`, and
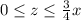`\(0 \leq z \leq (3)/(4)x\)`. The density
`\(\delta\)` is given as 1.

`\[I_y = \int_0^8 \int_0^3 \int_0^{(3)/(4)x} [(y-3)^2 + z^2] \, dz \, dy \, dx\]`

By evaluating this triple integral, the moment of inertia about the y-axis is found to be
`\((91)/(3)\)`.

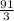This result indicates how the mass is distributed within the wedge about the specified axis. The expression
`\(I_L = (91)/(3)\)` represents the resistance of the solid wedge to changes in rotation about the line
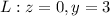`\(L: z=0, y=3\)`. The larger the moment of inertia, the more resistant an object is to changes in its rotational motion.