Question

Find derivative of y=√3 {sin / (7 x+1)}
a) {d y}{d x}={7cos (7 x+1)} / {3 sin (7 x+1)²/³

Answer 1

The derivative of
`\( y = \sqrt[3]{\sin(7x + 1)} \) with respect to \( x \) is \( (7\cos(7x + 1))/(3\sin^(2/3)(7x + 1)) \).`

Step-by-step explanation

To find the derivative of
`\( y = \sqrt[3]{\sin(7x + 1)} \) with respect to \( x \), we'll use the chain rule. Let \( u = 7x + 1 \), then \( y = \sqrt[3]{\sin(u)} \).` Applying the chain rule, the derivative
`\( (dy)/(dx) \) is given by \( (1)/(3)\sin^(-2/3)(u) \cdot \cos(u) \cdot (du)/(dx) \). Now, \( (du)/(dx) = 7 \), so substituting back, we get \( (dy)/(dx) = (7\cos(7x + 1))/(3\sin^(2/3)(7x + 1)) \).`

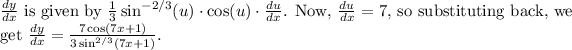
In the numerator,
`\( 7\cos(7x + 1) \)`represents the derivative of the inner function
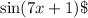`\( \sin(7x + 1) \`), and in the denominator,
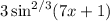`\( 3\sin^(2/3)(7x + 1) \)`accounts for the chain rule's contribution involving the cube root and the sine function. The result is a concise expression capturing the rate of change of the given function with respect to x .

This derivative is particularly useful in understanding how the function behaves and how its rate of change varies with different values of x . The presence of trigonometric and root functions necessitates the application of the chain rule for an accurate calculation of the derivative.