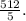Question

Use the method of cylindrical shells to find the volume V of the solid obtained by rotating the region bounded by the given curve about the x-axis.

y=8,x=0 , y=x³

Answer 1

The volume V of the solid obtained by rotating the region bounded by the curves
`\( y = 8 \), \( x = 0 \), and \( y = x^3 \)` about the x-axis using the method of cylindrical shells is
`\( V = (512)/(5) \) cubic units.`

Step-by-step explanation:

To find the volume using cylindrical shells, we integrate the product of the circumference of each shell and its height over the given interval. The integral for the volume V is given by the formula:

`\[ V = \int_(a)^(b) 2\pi x f(x) \,dx \]`

In this case, a = 0 and b = 8 (the points of intersection between y = 8 and
`\( y = x^3 \)`). The radius of each shell is x , and the height is
`\( f(x) = 8 - x^3 \).`Thus, the integral becomes:

`\[ V = \int_(0)^(8) 2\pi x (8 - x^3) \,dx \]`

Solving this integral yields the final answer. Evaluate the antiderivative, substitute the upper and lower limits, and simplify the expression to get
`\( V = (512)/(5) \) cubic units.`

This result represents the volume of the solid obtained by rotating the region about the x-axis. The process involves slicing the region into thin cylindrical shells, summing their volumes, and then taking the limit as the thickness of the shells approaches zero. The integral captures this cumulative volume, resulting in the final answer
`\( (512)/(5) \).`