Question

Find the domain of the function f(x)=(7)/(x-2)

Answer 1

The domain of the function f(x) = 7/(x-2) is all real numbers except x ≠ 2.

Step-by-step explanation:

The domain of a function represents the set of valid input values for which the function is defined. In the case of the function
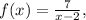`\(f(x) = (7)/(x-2)\),` the denominator
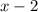`\(x-2\)` must not equal zero to avoid division by zero, as this operation is undefined in mathematics.

Setting
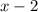`\(x-2\)` equal to zero and solving for x, we find that
`\(x = 2\)` makes the denominator zero. Consequently, the function is undefined at
`\(x = 2\)` . Therefore, the domain of the function excludes
`\(x = 2\)` , and we express this as
`\(x \in \mathbb{R}\)` where
`\(\mathbb{R}\)` denotes the set of all real numbers, excluding
`\(x \\eq 2\)`

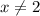
This restriction ensures that the function is well-defined for all other real values of x, emphasizing the importance of avoiding situations where the denominator becomes zero to maintain mathematical coherence and validity.