Question

Find the derivative of the function y=3 x eˣ⁵.
d y/d x=

Answer 1

The derivative of the function
`y = 3xe^(5x)` with respect to x is dy/dx =
`3e^(5x) + 15x e^(5x).`

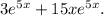
Step-by-step explanation:

When finding the derivative of the given function,
`y = 3xe^(5x)`, we apply the product rule, which states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.

In this case, the derivative involves the product of two functions
`3x` and
`e^(5x)`. The derivative of the first function (3x) is 3, and the derivative of the second function
`(e^(5x)) 5e^(5x)`. Applying the product rule, we get the expression
`3e^(5x) + 15xe^(5x)`as the derivative of the given function.

Therefore, the final answer for the derivative dy/dx is
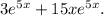`3e^(5x) + 15x e^(5x).` This result represents the rate of change of the original function with respect to x.